যদি পৃথিবী থেমে যেত — মহাকাশের অদ্ভুত নৃত্য

✍ লেখক: প্রদ্যুৎ আচার্য – MyAstrology, Astrologer & Palmist

ভূমিকা ও কৌতূহলী প্রশ্ন - Vedic Astronoy

আমরা সকলেই জানি—মহাকাশে কিছুই স্থির নয়। সৌরমণ্ডল যেন এক বিশাল সঙ্গীতানুষ্ঠান, যেখানে প্রতিটি গ্রহ তার নিজস্ব ছন্দে তালে মেতে নাচছে। সূর্যকে কেন্দ্র করে পৃথিবীর অবিরাম ঘূর্ণন, চাঁদের ধীরলয়ে প্রদক্ষিণ, আর নক্ষত্রদের নীরব জ্বলজ্বলে উপস্থিতি—সবই মিলিয়ে যেন এক মহাজাগতিক কাব্য।

কিন্তু ভাবুন তো—যদি একদিন এই নাট্যমঞ্চের মূলে থাকা পৃথিবীকে আমরা একেবারে থামিয়ে দিই? যদি সে আর ঘুরে না, না প্রদক্ষিণ করে? তাহলে আকাশের দৃশ্য কি আগের মতোই থাকবে, নাকি বদলে যাবে প্রতিটি গ্রহ-নক্ষত্রের নৃত্যের ধারা? এ প্রশ্ন শুধু বৈজ্ঞানিক নয়, গভীর দার্শনিক ও—কারণ এতে লুকিয়ে আছে আমরা "বাস্তব" বলে যা দেখি তার আসল রূপ।

সৌরমণ্ডল ও পৃথিবী-চন্দ্র সম্পর্ক

সৌরমণ্ডলের কেন্দ্রে অবস্থান করছে সূর্য—এক দীপ্তিমান মহাশক্তির গোলক, যার মহাকর্ষে আবদ্ধ রয়েছে আটটি গ্রহ, অসংখ্য উপগ্রহ ও নক্ষত্রখচিত ধূলিকণা। পৃথিবী প্রতি বছর সূর্যের চারদিকে ঘুরে আসে প্রায় ৩৬৫ দিন ৫ ঘণ্টা ৪৮ মিনিটে—যা আমাদের "সূর্য বৎসর"। চাঁদ, আমাদের নিকটতম মহাজাগতিক সঙ্গী, পৃথিবীর চারদিকে প্রদক্ষিণ অর্থাৎ এক চক্কর দেয় প্রায় ২৭.৩ দিনে, কিন্তু পূর্ণিমা থেকে পূর্ণিমা যেতে সময় লাগে প্রায় ২৯.৫ দিন—এটাই "সিনোডিক মাস "।

যদি পৃথিবী স্থির থাকত? – Geocentric Model

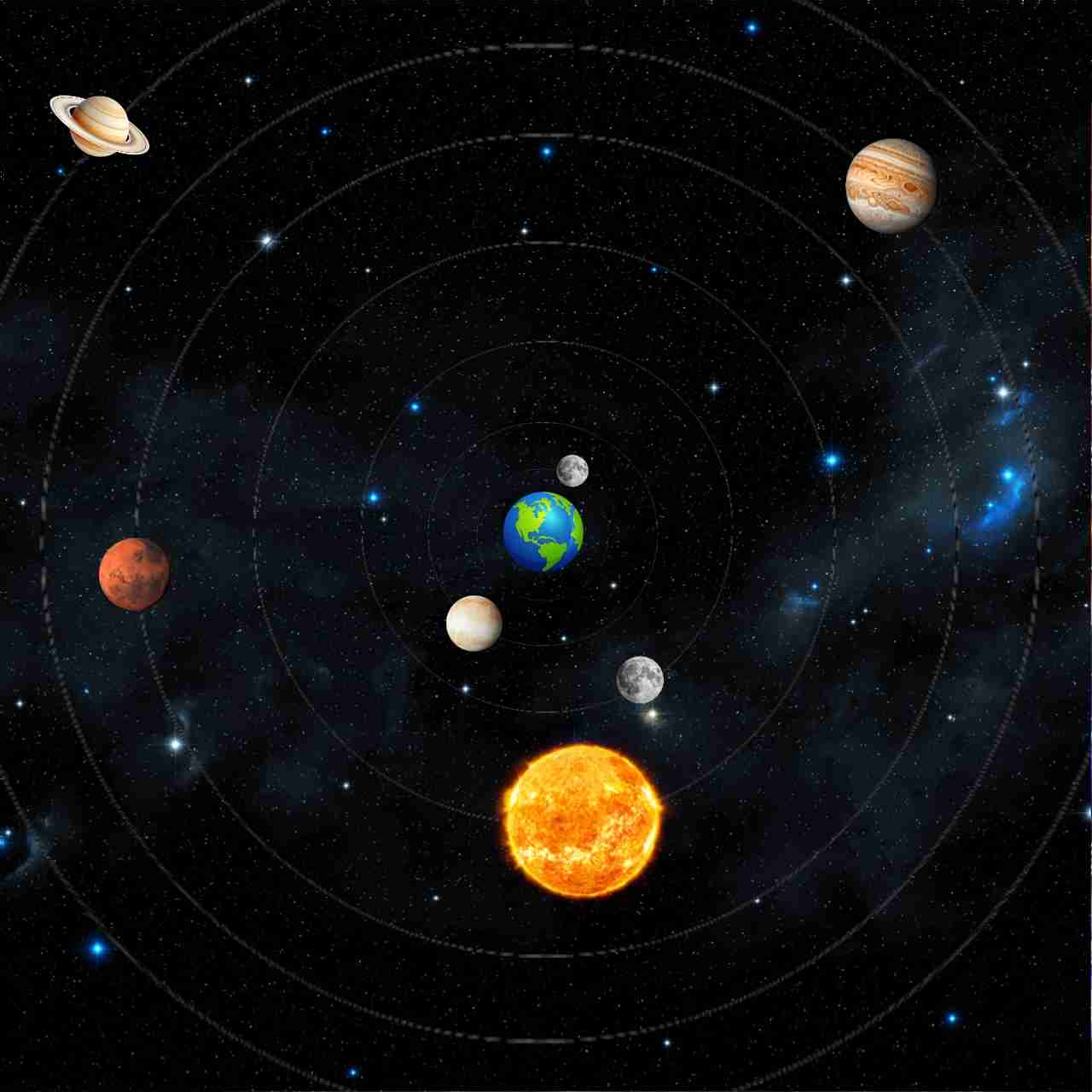
পৃথিবীকে যদি আমরা স্থির ধরি, তবে সূর্য, চাঁদ ও সমস্ত গ্রহ-নক্ষত্র যেন প্রতিদিন আকাশে তার চারপাশে ঘুরছে বলে মনে হবে। এ দৃশ্য প্রাচীন ভারতীয় জ্যোতির্বিদরা পৃথিবী-কেন্দ্রিক মডেল (Geocentric Model) দিয়ে ব্যাখ্যা করতেন। সূর্যসিদ্ধান্ত ও আর্যভটীয়-এর পাতায় আমরা পাই আকাশের এমন এক মানচিত্র, যেখানে সূর্য প্রতিদিন পূর্ব থেকে উঠে পশ্চিমে ডোবে, চাঁদ রাশিচক্রে দ্রুত ছুটে যাবে, আর মঙ্গল, বৃহস্পতি, শনি—সবাই তাদের নিজস্ব পথ ধরে ধীরে ধীরে অগ্রসর হবে।

আধুনিক বিজ্ঞান আমাদের বলেছে, আসলে পৃথিবীই ঘুরছে—কিন্তু দার্শনিকভাবে দেখলে, এই পার্থক্য আমাদের শেখায় যে "দৃষ্টি" ও "বাস্তবতা" সবসময় একই নয়। আমরা যা দেখি, তা হয়তো এক ভ্রম, কিন্তু সেই ভ্রমও আমাদের চিন্তা ও কল্পনার দরজা খুলে দেয়।

পৃথিবী স্থির ধরে মহাকাশের দৃশ্য — Geocentric Model, Apparent Motion ও Retrograde Motion

Geocentric Model-এর ধারণা

মানুষের আকাশ পর্যবেক্ষণের ইতিহাসে এক সময়ে সবচেয়ে জনপ্রিয় মডেল ছিল Geocentric Model — অর্থাৎ পৃথিবী মহাবিশ্বের কেন্দ্র, আর সূর্য, চাঁদ, গ্রহ ও নক্ষত্র সবাই পৃথিবীর চারপাশে ঘুরছে।

এই ধারণা গ্রিক জ্যোতির্বিদ ক্লডিয়াস টলেমি (Claudius Ptolemy)-এর Almagest গ্রন্থে অত্যন্ত বিশদভাবে বর্ণিত হয়েছে। ভারতীয় জ্যোতির্বিজ্ঞানেও, বিশেষ করে সূর্যসিদ্ধান্ত ও আর্যভটীয় গ্রন্থে, পৃথিবী-কেন্দ্রিক পর্যবেক্ষণের বর্ণনা পাওয়া যায়।

এই মডেলে প্রতিদিন সূর্য, চাঁদ, গ্রহ, এমনকি পুরো নক্ষত্রপটকেও মনে হয় পূর্ব থেকে পশ্চিম দিকে ঘুরছে — যা আসলে পর্যবেক্ষকের দৃষ্টিকোণ থেকে সৃষ্ট একটি ধারণা।

আপাত গতি (Apparent Motion)

আমরা আকাশের দিকে তাকিয়ে যে গতি দেখি, তা আসলে আপাত গতি — বাস্তব গতি নয়, বরং পর্যবেক্ষকের দৃষ্টিকোণ থেকে দেখা গতি।

উদাহরণ: আপনি যদি চলন্ত গাড়িতে বসে পাশের মাঠ দেখেন, মনে হবে গাছগুলো পিছনে চলে যাচ্ছে। বাস্তবে গাছ স্থির, আপনি এগোচ্ছেন।

Geocentric Model-এ ঠিক এইভাবেই মনে হয় — সূর্য, চাঁদ, গ্রহ ও নক্ষত্র সবাই আমাদের চারপাশে ঘুরছে, যদিও বাস্তবে পৃথিবী নিজেই ঘুরছে।

Retrograde Motion — গ্রহের পিছনে চলা বক্র গতি

সবচেয়ে রহস্যময় ও কৌতূহল উদ্দীপক ঘটনা হলো Retrograde Motion — যেখানে দেখা যায়, কোনো গ্রহ কিছুদিনের জন্য উল্টো দিকে চলছে। এই ঘটনা বিশেষ করে মঙ্গল, বৃহস্পতি ও শনির মতো বাইরের গ্রহের ক্ষেত্রে বেশি দেখা যায়।

Geocentric Model এই ঘটনাকে ব্যাখ্যা করেছিল Epicycle (ছোট বৃত্ত) ও Deferent (বড় বৃত্ত)-এর ধারণা দিয়ে। অর্থাৎ, গ্রহ একটি বড় বৃত্ত বরাবর ঘোরার পাশাপাশি একটি ছোট বৃত্তেও ঘোরে, যার ফলে মাঝে মাঝে উল্টো দিকে চলা মনে হয়।

উদাহরণ: ভাবুন, আপনি দৌড় প্রতিযোগিতায় আছেন এবং পাশের লেনে ধীরে চলা একজনকে ওভারটেক করলেন। ওভারটেক করার মুহূর্তে মনে হবে — সে আপনার তুলনায় কিছুক্ষণের জন্য পিছনে যাচ্ছে। আকাশে বাইরের গ্রহদের Retrograde Motion ঠিক এরকমই দেখায়।

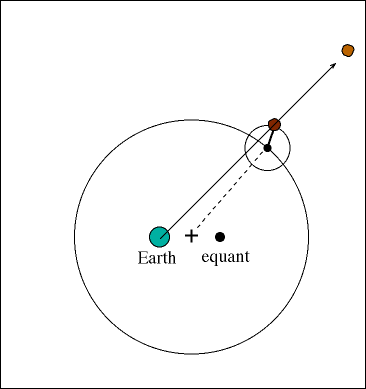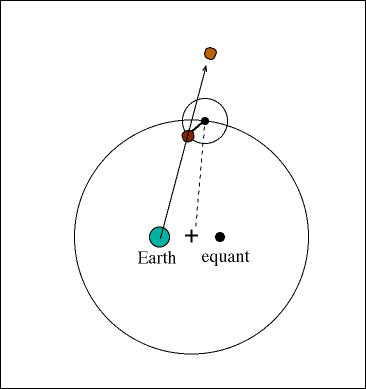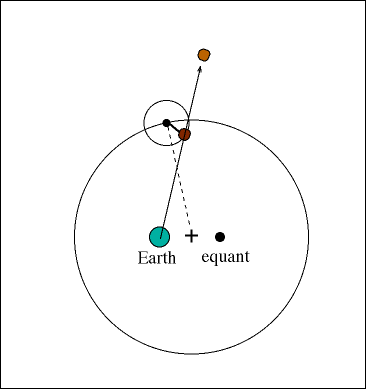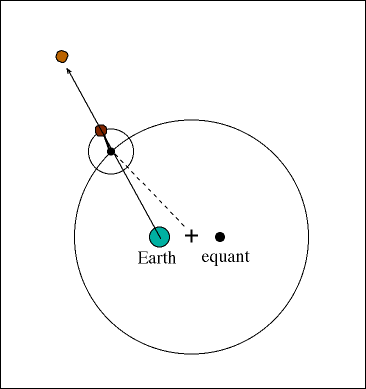
ছবির সূত্র: NASA ও ISRO-এর প্রকাশিত সৌরজগতের গ্রাফিক্স অথবা স্বতন্ত্র ইলাস্ট্রেশন।

সূর্য-কেন্দ্রিক বনাম পৃথিবী-কেন্দ্রিক গণনা — Heliocentric ও Geocentric তুলনা

১. Heliocentric বনাম Geocentric — মৌলিক ধারণা

Heliocentric Model: ১৫৪৩ সালে নিকোলাস কপারনিকাস (Nicolaus Copernicus) তাঁর বই De revolutionibus orbium coelestium-এ প্রস্তাব করেন যে, সূর্য সৌরমণ্ডলের কেন্দ্র এবং সমস্ত গ্রহ (পৃথিবীসহ) সূর্যের চারদিকে ঘোরে। পৃথিবী প্রতিদিন নিজ অক্ষে ঘোরে (Rotation) এবং বছরে একবার সূর্যের চারদিকে ঘোরে (Revolution)।

Geocentric Model: প্রাচীন গ্রিস ও ভারতীয় জ্যোতির্বিজ্ঞানে জনপ্রিয় ছিল। পৃথিবীকে স্থির ধরে সূর্য, চাঁদ ও গ্রহদের পৃথিবীর চারপাশে ঘুরতে দেখা যায়। গ্রিক জ্যোতির্বিদ Claudius Ptolemy-এর Almagest ও ভারতীয় সূর্যসিদ্ধান্ত-এ এর বিশদ বর্ণনা রয়েছে।

২. সময় ও গতির পার্থক্য — দুই মডেলের দৃষ্টিতে

Geocentric Model-এ গ্রহদের আপাত গতি বোঝাতে “Epicycle” এবং “Deferent” ধারণা ব্যবহার করা হয়।

Heliocentric Model-এ গ্রহের গতি ব্যাখ্যা করা হয় সরল কক্ষপথ দিয়ে, যেখানে জোহানেস কেপলার (Johannes Kepler)-এর তিনটি সূত্র প্রযোজ্য:

• কক্ষপথ উপবৃত্তাকার (Elliptical Orbit)
• সমান সময়ে সমান ক্ষেত্রফল অতিক্রম (Equal Areas in Equal Time)
• কক্ষপথের সময়ের বর্গ ∝ দূরত্বের ঘন (T² ∝ R³)

৩. কোনটি বৈজ্ঞানিকভাবে সঠিক?

আধুনিক জ্যোতির্বিজ্ঞান, ISRO ও NASA-এর সব গবেষণা Heliocentric Model-এর উপর ভিত্তি করে। পর্যবেক্ষণ ও গণনা পুরোপুরি মিলেছে। স্যাটেলাইট, স্পেস প্রোব ও গ্রহ মিশনের সঠিক পথ নির্ধারণ শুধুমাত্র সূর্য-কেন্দ্রিক পদ্ধতিতেই সম্ভব। Geocentric Model পর্যবেক্ষণ-ভিত্তিক হলেও প্রকৃত গতি বোঝায় না।

৪. তুলনামূলক টেবিল

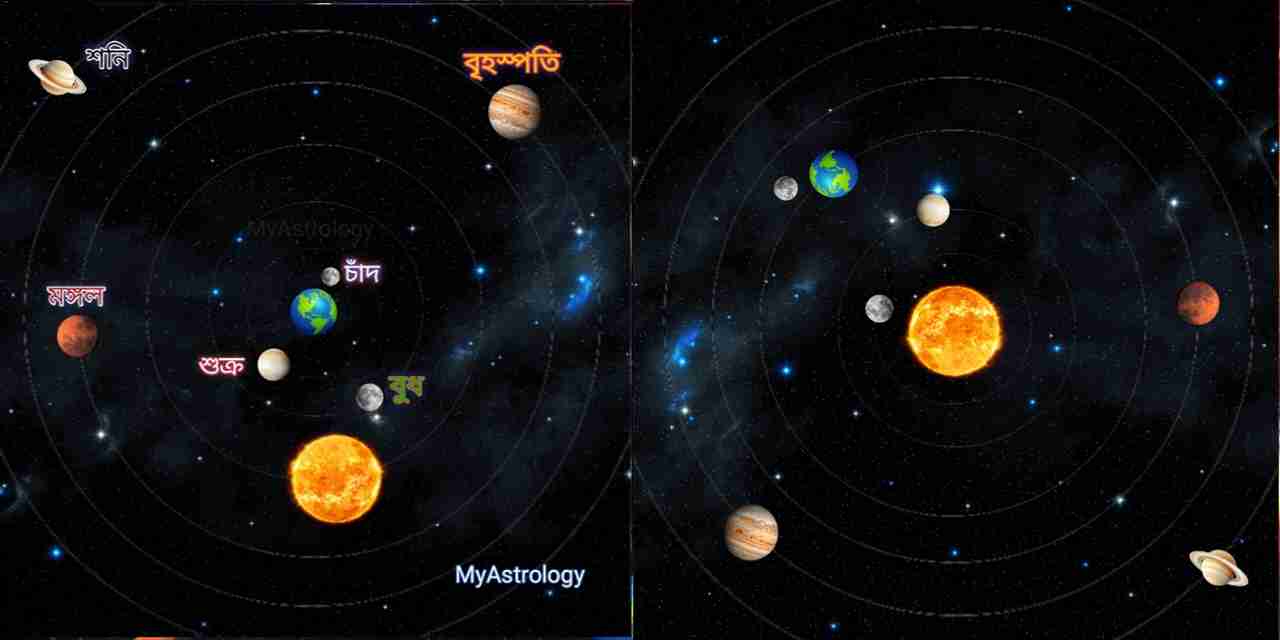
সূত্র: Copernicus (1543) — De revolutionibus orbium coelestium, Claudius Ptolemy — Almagest, ISRO & NASA Solar System Graphics

🌞 সূর্য-কেন্দ্রিক গ্রহের গতি ও সময় (Heliocentric Period)

১. Heliocentric Period কী?

ভাবুন, আপনি সূর্যের উপর দাঁড়িয়ে আছেন। চারপাশে বুধ, শুক্র, পৃথিবী, মঙ্গল, বৃহস্পতি… সব গ্রহ তাদের নিজ নিজ পথে ঘুরছে।

Heliocentric Period মানে হলো — কোনো গ্রহ সূর্যের চারদিকে একবার পূর্ণ ঘুরে আসতে যত সময় নেয়।

পৃথিবীর জন্য এটি ১ বছর বা প্রায় ৩৬৫ দিন। কিন্তু প্রতিটি গ্রহের এই সময় আলাদা, কারণ সূর্য থেকে তাদের দূরত্ব ভিন্ন।

২. Kepler’s Third Law – খুব সহজ ভাষায়

জ্যোতির্বিদ Johannes Kepler ৪০০ বছর আগে বলেছিলেন —

"গ্রহ যত দূরে, তার ঘুরতে তত বেশি সময় লাগে।"

তাঁর তৃতীয় সূত্র:

T² ∝ R³

• T = একবার ঘুরতে সময় (পৃথিবীর বছর হিসেবে)
• R = সূর্য থেকে গড় দূরত্ব (AU — Astronomical Unit)
• ১ AU = পৃথিবী থেকে সূর্যের গড় দূরত্ব (~১৪৯.৬ মিলিয়ন কিমি)

সহজ উদাহরণ:

পৃথিবী → R = 1 AU, T = 1 বছর

মঙ্গল (Mars) → R = 1.524 AU

গণনা:

1. R³ = 1.524³ ≈ 3.54
2. T² = 3.54 ⇒ T = √3.54 ≈ 1.88 বছর

অর্থাৎ, মঙ্গল সূর্যকে একবার ঘুরতে প্রায় ১ বছর ১১ মাস সময় নেয়।

৩. NASA Planetary Fact Sheet – গ্রহের কক্ষপথকাল

৪. কক্ষপথের আকার – চিত্র ব্যাখ্যা

সব গ্রহ উপবৃত্তাকার (Elliptical) কক্ষপথে ঘোরে, যেখানে সূর্য থাকে উপবৃত্তের এক ফোকাসে।

• Perihelion (সূর্যের কাছাকাছি) → গ্রহ দ্রুত চলে
• Aphelion (সূর্য থেকে দূরে) → গ্রহ ধীরে চলে

Kepler’s 2nd Law বলছে — গ্রহ সমান সময়ে সমান ক্ষেত্রফল অতিক্রম করে।

৫. কেন এই সময় জানা দরকার?

• মহাকাশযান পাঠানোর সঠিক সময় নির্ধারণ
• গ্রহের অবস্থান ও ঋতু গণনা
• জ্যোতিষশাস্ত্রে গ্রহের সঠিক অবস্থান নির্ধারণ

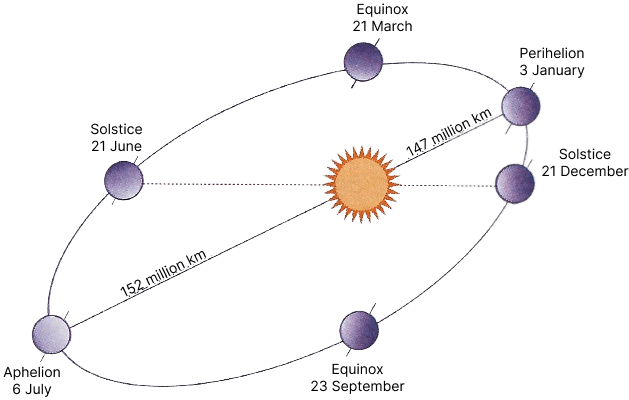
সূত্র: Johannes Kepler — Harmonices Mundi (1619), NASA — Solar System Exploration, ISRO — Space Science Data

🌍 পৃথিবী-কেন্দ্রিক গ্রহের গতি ও সময় (Synodic Period)

১. Synodic Period কী?

ভাবুন, আপনি পৃথিবীতে দাঁড়িয়ে আকাশ দেখছেন। কোনো গ্রহ কখনো সূর্যের একপাশে, কখনো অন্যপাশে দেখা যায়। Synodic Period মানে হলো —

"পৃথিবী থেকে দেখা কোনো গ্রহের একই অবস্থানে (যেমন Opposition বা Conjunction) ফিরে আসতে যত সময় লাগে।"

পার্থক্য মনে রাখুন:

• Heliocentric Period → সূর্যের দৃষ্টিতে গ্রহের একবার ঘোরা
• Synodic Period → পৃথিবীর দৃষ্টিতে গ্রহের একবার “পুনরায় দেখা”

২. উদাহরণ – মঙ্গল গ্রহ

Heliocentric Period (Tₘ) = 1.88 বছর
পৃথিবীর Period (Tₑ) = 1 বছর

সূত্র:

1/S = | (1/Tₑ) - (1/Tₘ) |
  

গণনা:

1. 1/Tₑ = 1
2. 1/Tₘ = 1 / 1.88 ≈ 0.532
3. পার্থক্য = 1 - 0.532 = 0.468
4. S = 1 / 0.468 ≈ 2.136 বছর

অর্থাৎ, পৃথিবী থেকে মঙ্গলকে একই অবস্থানে ফিরতে দেখতে প্রায় ২ বছর ৫০ দিন লাগে।

৩. কেন পার্থক্য হয়? – Relative Motion

মূল কারণ হলো Relative Speed বা আপেক্ষিক গতি। সূর্যকে কেন্দ্র ধরে সব গ্রহ আলাদা গতিতে ঘুরছে। পৃথিবীও চলমান, তাই পৃথিবী থেকে গ্রহগুলির গতি কখনো “মিলিত” (ভেতরের গ্রহ), কখনো “বিয়োগ” (বাইরের গ্রহ) আকারে দেখা যায়।

• বাইরের গ্রহ (Mars, Jupiter, Saturn…) → পৃথিবী দ্রুত ঘোরে, তাই বারবার “ওভারটেক” করে।
• ভেতরের গ্রহ (Mercury, Venus) → তারা দ্রুত ঘোরে, তাই বারবার পৃথিবীকে “ওভারটেক” করে।

৪. বাইরের ও ভেতরের গ্রহ – Synodic Period তুলনা (NASA Data)

৫. Retrograde Motion ও Synodic Period

বাইরের গ্রহ যখন পৃথিবী “ওভারটেক” করে, তখন আকাশে তারা কিছুদিনের জন্য পেছনে চলা (Retrograde) মনে হয়।

এই “পেছনে যাওয়া” সময় Synodic Periodের অংশ। উদাহরণস্বরূপ, মঙ্গল প্রায় ৭২ দিন Retrograde থাকে, যা প্রতি ৭৮০ দিনে (তার Synodic Period) একবার ঘটে।

৬. চিত্র ধারণা

৭. ব্যবহার ও গুরুত্ব

• জ্যোতির্বিদ্যার পর্যবেক্ষণ পরিকল্পনা
• গ্রহের দর্শনীয় সময় পূর্বাভাস
• জ্যোতিষশাস্ত্রে গ্রহের সঠিক অবস্থান নির্ধারণ

সূত্র: NASA — Solar System Dynamics, ISRO Space Applications Centre, Jean Meeus — Astronomical Algorithms

♈ রাশিচক্র ও গ্রহের প্রদক্ষিণ সময়

১. রাশিচক্র (Zodiac) ও গ্রহের গতি পথ

রাশিচক্র হল আকাশের ৩৬০° একটি কাল্পনিক বৃত্ত, যা ১২টি সমান ভাগে বিভক্ত — প্রতিটি ৩০° করে। প্রতিটি ভাগ একটি রাশি নামে পরিচিত (মেষ ♈ থেকে মীন ♓ পর্যন্ত)।

সূর্য, চন্দ্র ও গ্রহগুলো এই বৃত্ত বরাবরই চলে, যাকে আমরা ক্রান্তিবৃত্ত (Ecliptic) বলি।

২. Sidereal Period বনাম Synodic Period

Sidereal Period = “আসল” একবার ঘোরা (প্রকৃত কক্ষপথকাল)
Synodic Period = “আমাদের চোখে” একবার ফিরে আসা (আপেক্ষিক অবস্থানকাল)

৩. রাশিচক্র অনুযায়ী সময় গণনা

বৈদিক জ্যোতিষে প্রতিটি গ্রহকে একটি রাশি পার হতে যত সময় লাগে তা তার Sidereal Period এর উপর নির্ভর করে। নিচের টেবিলটি গড় মান (Heliocentric data) অনুসারে:

৪. সূর্য-কেন্দ্রিক ও পৃথিবী-কেন্দ্রিক পার্থক্যের কারণ

• 🔸 Heliocentric → গ্রহের প্রকৃত কক্ষপথ ও সময় (Sidereal Period) নির্ধারণ হয়, আধুনিক জ্যোতির্বিজ্ঞান এই পদ্ধতি ব্যবহার করে।
• 🔸 Geocentric → পর্যবেক্ষক পৃথিবীতে থাকায় Synodic Period মাপা হয়, যেখানে Retrograde ও Stationary আপাত পরিবর্তন দেখা যায়।

৫. উদাহরণ – বৃহস্পতির ক্ষেত্রে

Sidereal Period → 11.86 বছর (সূর্য-কেন্দ্রিক)
Synodic Period → 1.092 বছর (~399 দিন, পৃথিবী থেকে দেখা)

মানে, বৃহস্পতি আবার একই রাশিতে ফিরতে ~12 বছর লাগে, কিন্তু পৃথিবী থেকে নির্দিষ্ট অবস্থান মিলতে বছরে একবারের মতো দেখা যায়।

৬. Vedic Astrology-তে প্রয়োগ

বৈদিক জ্যোতিষে:

• গ্রহের রাশি পরিবর্তন (Transits) পূর্বাভাসে Sidereal Time গুরুত্বপূর্ণ।
• তিথি, নক্ষত্র, যোগ, করণ ইত্যাদি দৈনিক পঞ্জিকা তৈরিতে Geocentric Position ব্যবহার হয়।
• উদাহরণ: শনি প্রায় ২.৫ বছর এক রাশিতে থাকে, তাই “শনি সাড়ে সাতি” গণনায় রাশি ও ডিগ্রির সঠিক অবস্থান জরুরি।

সূত্র: NASA Solar System Exploration, ISRO, US Naval Observatory

🌞 সূর্য বৎসর ও 🌙 চন্দ্র বৎসরের পার্থক্য

১. সূর্য বৎসরের সংজ্ঞা (Solar Year)

সূর্য বৎসর হলো পৃথিবী সূর্যের চারদিকে একবার পূর্ণ প্রদক্ষিণ করতে যে সময় নেয়।

• সময়: ৩৬৫ দিন ৫ ঘণ্টা ৪৮ মিনিট ৪৬ সেকেন্ড
• দিন হিসাবে: ৩৬৫.২৪২২ দিন
• এই হিসাব পৃথিবীর কক্ষপথের গতি বা Tropical Year থেকে নেওয়া হয়।
• আধুনিক গ্রেগরিয়ান ক্যালেন্ডার এই সময় অনুসরণ করে।

২. চন্দ্র বৎসরের সংজ্ঞা (Lunar Year)

চন্দ্র বৎসর হলো চাঁদের এক পূর্ণ চক্র (নতুন চাঁদ থেকে নতুন চাঁদ) গড়ে ১২ বার সম্পন্ন হওয়ার মোট সময়।

• এক চন্দ্র মাসের গড় দৈর্ঘ্য (Synodic Month): ২৯ দিন ১২ ঘণ্টা ৪৪ মিনিট ৩ সেকেন্ড
• ১২টি চন্দ্র মাসের মোট সময়: ৩৫৪ দিন ৮ ঘণ্টা ৪৮ মিনিট ৩৬ সেকেন্ড
• দিন হিসাবে: প্রায় ৩৫৪.৩৬ দিন
• সূত্র: NASA Moon Fact Sheet

অর্থাৎ, চন্দ্র বছর সূর্য বছরের তুলনায় প্রায় ১০ দিন ২১ ঘণ্টা ছোট।

৩. সময়ের পার্থক্য – টেবিল

৪. বৈজ্ঞানিক কারণ

• ☀️ সূর্য বৎসর নির্ভর করে পৃথিবীর সূর্যের চারদিকে কক্ষপথে একবার ঘোরার উপর।
• 🌙 চন্দ্র বৎসর নির্ভর করে চাঁদের পৃথিবীর চারদিকে ঘোরা ও সূর্যের সাথে আপেক্ষিক অবস্থান পরিবর্তনের উপর।
• পৃথিবীর কক্ষপথ চলমান হওয়ায় চাঁদের চক্র ও সূর্য বৎসরের সময় মিলে যায় না।

৫. অধিমাস বা মলমাসের ভূমিকা

চন্দ্র বছর সূর্য বছরের চেয়ে ছোট হওয়ায়, হিন্দু পঞ্জিকায় প্রায় ৩ বছরে একবার অতিরিক্ত মাস যোগ করা হয়, যাকে অধিমাস বা মলমাস বলা হয়।

এর ফলে উৎসব ও ঋতুর সামঞ্জস্য থাকে — যেমন, দুর্গাপূজা সবসময় শরৎ ঋতুতেই আসে।

🌙 চন্দ্র তিথি ও হিন্দু উৎসবের তারিখ পরিবর্তন

১. তিথি কী?

তিথি হলো চাঁদের সূর্যের সাথে আপেক্ষিক কৌণিক দূরত্ব (Angular Distance) ১২° বাড়তে যত সময় লাগে।

• এক পূর্ণ চন্দ্রচক্রে ৩০টি তিথি হয় — শুক্লপক্ষ (নতুন চাঁদ → পূর্ণিমা) ১৫টি এবং কৃষ্ণপক্ষ (পূর্ণিমা → নতুন চাঁদ) ১৫টি।
• একেক তিথির দৈর্ঘ্য সমান নয় — ২৩ ঘণ্টা ৩৭ মিনিট থেকে ২৫ ঘণ্টা পর্যন্ত হতে পারে।
• তিথি সবসময় সূর্যোদয় থেকে সূর্যোদয় পর্যন্ত মেলে না, তাই উৎসবের গ্রেগরিয়ান তারিখ পরিবর্তিত হয়।

২. কেন তিথি পরিবর্তন হয়?

• চাঁদের কক্ষপথ উপবৃত্তাকার, তাই তার গতি কখনও বেশি, কখনও কম হয়।
• পৃথিবীর কক্ষপথের কারণে সূর্য ও চাঁদের আপেক্ষিক অবস্থান প্রতিদিন সমান হারে বদলায় না।
• ফলে একটি তিথি কখনও একদিনের মধ্যে শেষ হয়ে যায়, আবার কখনও দুই দিনে ভাগ হয়ে যায়।
• এই কারণেই দুর্গাপূজা, দীপাবলি, জন্মাষ্টমী প্রভৃতি উৎসব প্রতি বছর ভিন্ন তারিখে হয়।

৩. হিন্দু পঞ্জিকা গণনার নীতি

হিন্দু পঞ্জিকা চন্দ্র-সূর্যসিদ্ধ (Lunisolar) পদ্ধতিতে তৈরি হয়।

• মাস গণনা: নতুন চাঁদ (অমাবস্যা) বা পূর্ণিমা থেকে শুরু হয় — দুই ধরনের পঞ্জিকা প্রচলিত (অমান্ত ও পূর্ণিমান্ত)।
• তিথি গণনা হয় সূর্য ও চাঁদের দ্রাঘিমা (Longitude) পার্থক্য দিয়ে।

সূত্র:

তিথি সংখ্যা = (চাঁদের দ্রাঘিমা – সূর্যের দ্রাঘিমা) ÷ 12°

যখন এই পার্থক্য ১২°, ২৪°, ৩৬° … হয়, তখন নতুন তিথি শুরু হয়।

৪. অধিমাস বা মলমাস কীভাবে যোগ হয়

• এক চন্দ্র বছর = প্রায় ৩৫৪ দিন
• এক সূর্য বছর = প্রায় ৩৬৫ দিন
• পার্থক্য = প্রায় ১১ দিন

এই পার্থক্য জমে তিন বছরে প্রায় ৩০ দিন হয়।

যখন কোনও মাসে দুটি অমাবস্যা পড়ে কিন্তু মাঝখানে সূর্য সংক্রান্তি হয় না, তখন সেই মাসকে অধিমাস বলা হয়।

অধিমাসে কোনও বড় উৎসব হয় না, তবে ধর্মীয় অনুশীলন ও দানপুণ্যের জন্য শুভ ধরা হয়।

অধিমাস যোগের মাধ্যমে চন্দ্র ক্যালেন্ডার আবার সূর্য ক্যালেন্ডারের সাথে মেলানো হয়।

৫. বাস্তব উদাহরণ

যদি কোনও বছরে দুর্গাপূজা অক্টোবরে হয়, পরের বছরে তা সেপ্টেম্বর বা নভেম্বরেও হতে পারে — সবটাই তিথি ও সূর্যের আপেক্ষিক অবস্থানের উপর নির্ভর করে।

২০২০ সালে আশ্বিন মাসে অধিমাস হয়েছিল, তাই সেই বছরের কিছু উৎসব পরের বছরে এক মাস পিছিয়ে গিয়েছিল।

📚 Authentic References

• NASA – Moon Fact Sheet
• Vedic Heritage – Lunar-Solar Calendars
• TimeandDate – Hindu Calendar

🌟 জেনে রাখুন আরও গভীর সত্য

তিথি, গ্রহের গতি ও পঞ্জিকার সূক্ষ্ম গণনা শুধু অঙ্ক নয় – এগুলো আমাদের উৎসব ও জীবনের ছন্দের মূল রহস্য। MyAstrology – জ্যোতিষ ও হস্তরেখাবিদ্ ড. প্রদ্যুৎ আচার্য আপনাকে দেবেন বৈজ্ঞানিক যুক্তি ও প্রাচীন জ্ঞানের সমন্বয়ে নির্ভুল ব্যাখ্যা।

🔒 নিরাপদ অনলাইন পেমেন্ট | 📞 সরাসরি ফোন/হোয়াটসঅ্যাপ পরামর্শ